The Crisis. 1. The Identical Twin Vegan Study.

A recent identical twin-study comparing vegan and omnivore diets has gained some attention and a good deal of criticism.

Jul 07, 2024

A recent identical twin-study comparing vegan and omnivore diets has gained some attention and a good deal of criticism [1, 2, 3]. The conclusion, that vegan diets provide reduced CVD risk compared to an omnivore diet, is obviously controversial and, in my view, not justified. There are also fundamental errors in design and analysis, although some are correctable with further analysis. My main goal is to explain errors so that measurements and analyses can be done right in the future. The authors of the twin study have previously provided more substantive and balanced studies and it is assumed this paper was written in good faith but something went wrong here. It is important to straighten this out.

Group Statistics and Individual Data.

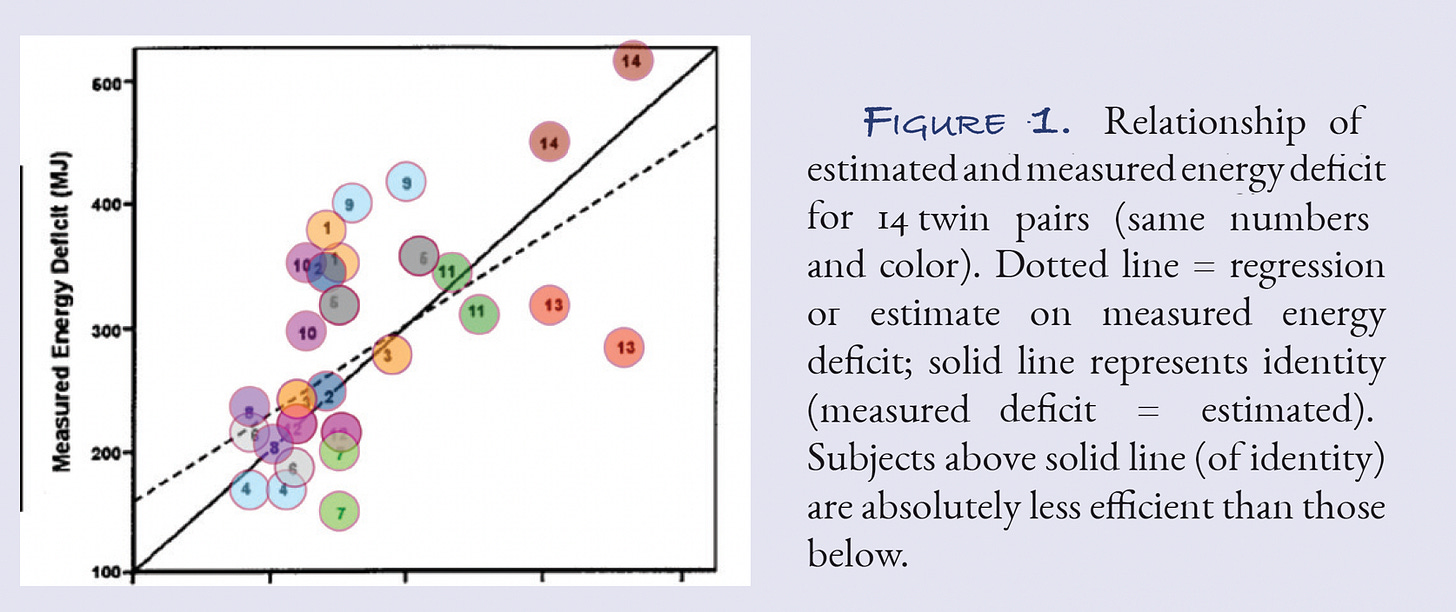
The fundamental error in design is that the diets to be compared are not overly different in composition — similar calories and macronutrients — and the major difference is the source of the protein, plant or animal. In the absence of any chemical detail about what the differences are, this is essentially just the name of the diet. In addition, the whole idea of a twin study is to control for genetics, upbringing and other biological factors that might affect the response to the diet. The results of such studies sensibly allow comparison of individual response. For example, a well known study from Allison’s group [4] compared change in body mass in twins bringing out the expected similarity in response between the two twins and the variability between sets of twins (Figure 1).

Oddly, Landry et al., grouped all subjects together reporting means of the outcome variablesr, vitiating the benefit of a teen study. (Table 1). The primary outcome, LDL-C had an average value of 95.5 mg/dL for vegans and 116.1 mg/dL for the omnivores, or 18 % lower for the vegans.

Often as they used, averages are not what’s called for. Nobody has an average LDL-C and the question is what were the individual values for vegans compared to those for omnivores. If we we only know about the group, how reliable are these numbers. In other words, is this to be expected for the next set of twins? Do any of the sets of twins go in the opposite direction? Further, along these lines, what is reported is not correct. Given that the individual values are not reported, the appropriate parameter to describe the reliability of the data is the standard deviation (SD). What the SD tells us is the spread of the values. For example, for a normal distribution, we know from the SD that 34% of the measured values fall on either side of the mean. That’s what we want to know. The values reported in Table 1, however, are the standard error of the mean (SEM) which tells us (theoretically) how the means of different samples would vary. Reporting standard error is misleading. This is pointed out in several publications:

….Now the sample mean will vary from sample to sample; the way this variation occurs is described by the “sampling distribution” of the mean. We can estimate how much sample means will vary from the standard deviation of this sampling distribution, which we call the standard error (SE) of the estimate of the mean [5].
The SEM is not a descriptive statistic. It tells us nothing about the sample. Therefore, it is illogical to state Mean (M) ± SEM when describing a sample; only M ± SD is correct. Then, when should the SEM be reported? A good answer could be “never” and the reason for this is that the SEM is best considered as an intermediate term in the calculation of 95% confidence interval (CI) and (where applicable) in the estimation of statistical significance [6].

SEM is not the appropriate parameter and is misleading because it always makes your data look better than it is. If you are reading a paper that reports SEM, you can calculate the value of the SD = √n x SEM, where n is the number of subjects. In Landry, n = 22 for each set of twins. The square root of 22 is 4.7, so looking at Table 1, The correct value for LDL-C is 95.5 ± (4.7 x 6.3) = 95.5 ± 29.5 mg/dL for vegans and 116.1 ± 34.4 mg/dL for omnivores. In other words, there is very large variation in the data and undoubtedly large overlap of the data suggesting caution in interpreting the results. Most of all, again, we don’t know the individual comparisons.

Thanks for reading Nutrition in Crisis! This post is public so feel free to share it.

A “diet” is not a biological variable.

The definition of particular diets is a common source of disagreement. Things are made worse when two diets are to be compared. Typically, ranges of macronutrients or dietary parameters are indicated and in, some cases, an outcome variable may define adherence. Compliance with a ketogenic diet, for example, has a built in measure in the blood level. The “diet” itself is not a biological variable and usually requires some description of the controlling variable. For example, in this groups' earlier work, the A-to-Z trial [7], different popular diets were compared and weight loss was tabulated over time (Figure 2A). This was a very telling study that did not receive appropriate attention possibly because the data strongly supported the Atkins diet and the authors presented a reasonable perspective on that diet, the bête noire of the medical orthodoxy:

“Concerns about adverse metabolic effects of the Atkins diet were not substantiated within the 12-month study period…. Physicians whose patients initiate a low-carbohydrate diet can be reassured that weight loss is likely to be at least as large as for any other dietary pattern and that the lipid effects are unlikely to be of immediate concern.”

Now, in the study, the diets were chosen among popular diets which referred to published information and the large separation in the outputs suggested that the study was going to be of value to end users. However, the key variable was likely dietary carbohydrate and one of the lipid variables that is substantially controlled by carbohydrate is triglycerides. The A-to-Z study also reported components of the diets as offered to the patients. I therefore took Gardner’s data and asked about the dependence of triglycerides on dietary carbohydrate. The results in Figure 2B show a remarkable linear response. The more carbohydrate, the more triglycerides. These points are averages but the linearity is quite remarkable.

The matrix method.

The ideal control for many biological experiments is a cross-over experiment where subjects serve as their own controls. Second best might be a twin study of the type under discussion. In the absence of these constraints, a simple way to compare individual performances in dietary (or other) trials, is the simple matrix method [7]. The rationale is that, since we don't know which subjects in intervention A should be matched with which subject in intervention B, all possibilities are shown. The individual results for the two diets are ordered according to the outcome of interest, for example, weight loss. The results for one diet, say very low carbohydrate ketogenic diet (LCKD), as in the published example from reference [8] shown in Figure 3, will be the x-axis of a rectangular matrix. The ordered outcomes for the other diet, low fat (LF) in the example, constitute the y-axis. All possible differences are calculated and these constitute the matrix elements. The matrix elements can be color coded to indicate particular levels of relative payoff, e.g. > 2 kg difference in weight loss. This provides a rough estimate of which strategy is likely to be better. The method has the advantage that it does not assume any particular distribution. It has the disadvantage that it assumes that the sample distribution of responses is somehow representative of the population distribution, and it therefore tends to over-emphasize differences (while standard statistics will emphasize similarities). We did not know this at the time — although we were sure it was related to some traditional method — but the procedure represents one of the early steps in the Wilcoxon statistic [10].

Testing the matrix netted,

The matrix method was tested by comparing the results with a cross-over experiment from Volek’s lab [8]. The fraction for which diet produced the greater weight loss was calculated from the matrix and from comparisons in the cross-over study. The agreement was good, fortuitously good for men, ratios of 73:27 for both methods. For women the ratios were 78:21 for matrix and 62:31 from the crossover

A similar test might be done for the Landry study and I have written to the authors to perform the test or share their data. The prediction is that in each pair of twins, LDL will be distinctly better than the corresponding omnivore diet. The results will also show what a more-or-less random outcome would be. Since the twin pairs are known, it can be seen how much has been gained by this procedure.

Leave a comment

Lessons from Landry, et al.

1. The diets: In my view, Landry, et al. is not well-conceived. In the comparison of a vegan diet with an omnivore diet, the emphasis is on the definite article. The diets are similar and if there is a difference it will be quite specific and it is impossible to tell what would happen if one or another parameter was changed. In other words, the criteria for assigning patients to one or another diet were too general. Almost by definition, an omnivore diet can include anything. The generalization that what was studied here is applicable to all diets identified as omnivore is not reasonable.

2. Standards. Medicine is full of arbitrary statistical methods, levels of evidence and “gold standards,” that is, analytic methods that apply to all experiments. This is unknown in any physical science. The best test is the one that answers the experimental question. If you say your diet is “the best,” critics will invoke “individualization” which is reasonable but it ask the question if your diet good for anybody and under what conditions. We need to see the individual data. Also, the principle of that SD, not SEM is the appropriate statistic for comparisons.

3. The community of scholars. Many people gain benefit in overall well-being and even therapeutic improvement in diabetes or obesity on vegetarian or vegan diets. However, the ‘Keypoints’ of this paper (possibly written by the editors) that “The findings from this trial suggest that a healthy plant-based diet offers a significant protective cardiometabolic advantage compared with a healthy omnivorous diet” is unwarranted. Whatever the success of vegan and vegetarian diets for adherents, a far greater number do better on other diets and the great majority of the country do not consider it as an option. In addition, it is abundantly clear that the message against meat, especially red meat, is highly politicized. In addition, the changes in the American diet in the past fifty years have been in the direction of red meat reduction and increase in vegetable consumption. No benefit in obesity and diabetes or other metabolic diseases has come from this behavior. Most of all, the majority of experimental studies do not support the conclusion. As described in court, you must produce exculpatory evidence.

In particular, the conclusion from Garner’s A-to-Z study is far more reasonable.

“Although a higher LDL-C concentration would appear to be an adverse effect, this may not be the case under these study condition. The triglyceride-lowering effect of a low-carbohydrate diet leads to an increase in LDL particle size, which is known to decreaseLDL atherogenicity. In the current study, at 2 months, mean LDL-C concentrations increased by 2% and mean triglyceride concentrations decreased by 30% in the Atkins group. … In addition, we examined non–HDL-C concentrations …and observed no significant differences among groups at any time point. Therefore, we interpret these findings to suggest that there were no adverse effects on the lipid variables for women following the Atkins diet compared with the other diets and, furthermore, no adverse effects were observed on any weight-related variable measured in this study at any time point for the Atkins group.”

References

Peter Ballerstedt

Jul 8, 2024

Today's entry for the "Well THAT'S awkward" folder-

"... the changes in the American diet in the past fifty years have been in the direction of red meat reduction and increase in vegetable consumption. No benefit in obesity and diabetes or other metabolic diseases has come from this behavior."

Expand full comment

1 reply by Richard Feinman